Central Limit Theorem
Function: calc[CLTdiscr] - Central Limit Theorem for discrete distributions
Calling Sequence:
CLTdiscr![]()
Parameters:
f - generating function for a discrete distribution
j - number of variables in the initial sum of the random variables
n - number of variables in the random sample
Stand = true/false , true: distributions are standardized, false: distributions are not standardized
Hist = true/false, true: plots histogram, ![]() : plots only the midpoint on the upper end of each rectangle of the histogram
: plots only the midpoint on the upper end of each rectangle of the histogram
K = false/k, if k = positive integer the histogram with constant width is plotted independent of the choices of ![]() and
and ![]() . Otherwise, select false
. Otherwise, select false
- CLTdiscr plots the distribution of the sum
![Y[k]](images/Some Pages_208.gif) =
= ![Sum(X[i], i = j .. k)](images/Some Pages_209.gif) ,
, 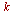 =
= 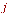 ,...,
,...,  as an animation. The plots are compared with the normal distribution with equal variance. All plots are located at the origin.
as an animation. The plots are compared with the normal distribution with equal variance. All plots are located at the origin.
Description:
Examples:
| > | restart: with(calc): |
| > | f:=t->.32*t^(-3)+.1*t^(-1)+.33*t+.1*t^3+.15*t^4; |
Some "messy" distribution
| > | CLTdiscr(f,1,20,true,true,false); |
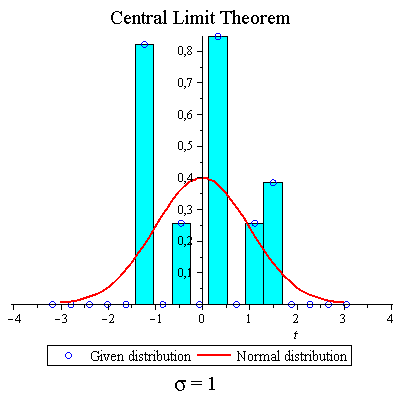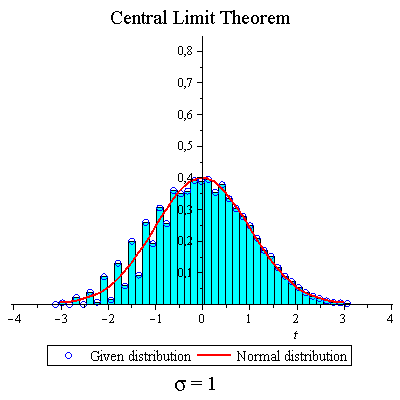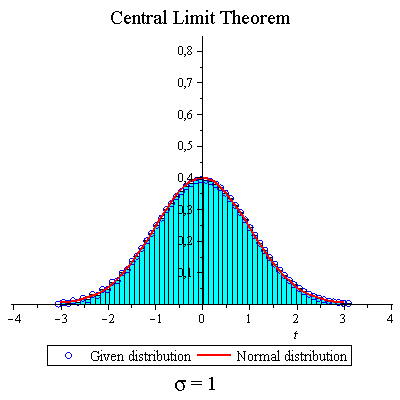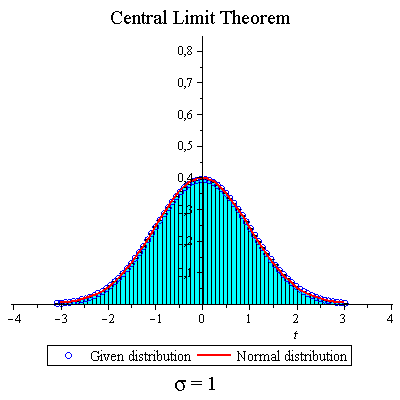 |
Skew binomial distribution
| > | f:=t->.7+.3*t; |
| > | CLTdiscr(f,1,40,true,true,false); |
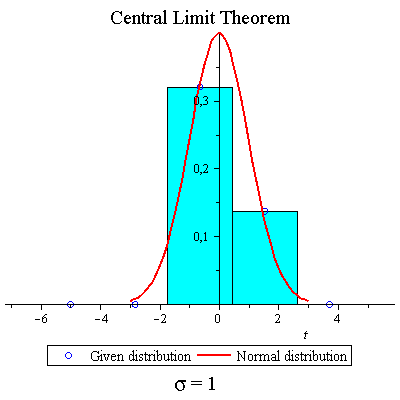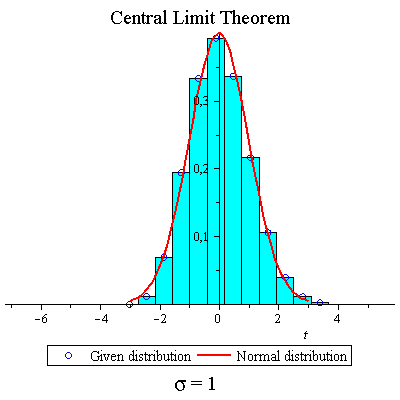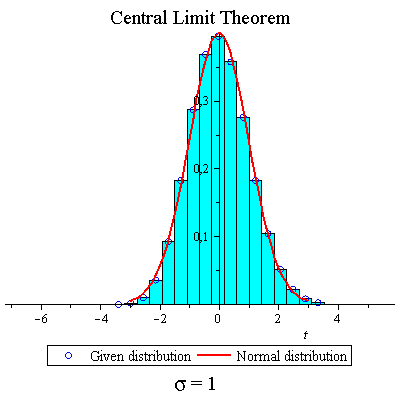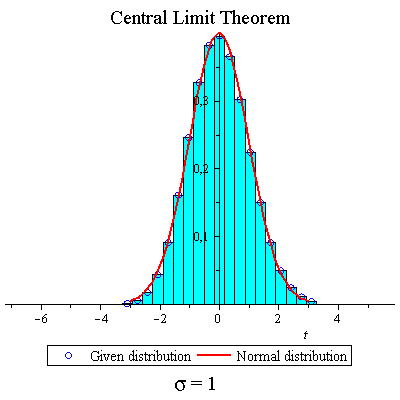 |
Throwing dice
| > | f:=t->1/6*t+1/6*t^2+1/6*t^3+1/6*t^4+1/6*t^5+1/6*t^6; |
| > | CLTdiscr(f,1,10,true,true,false); |
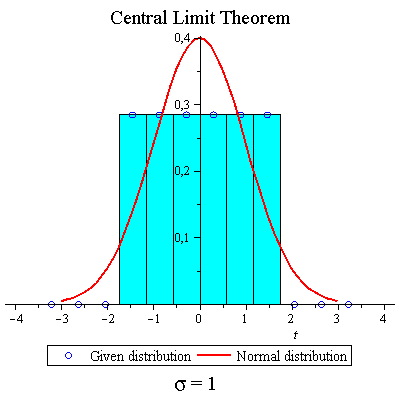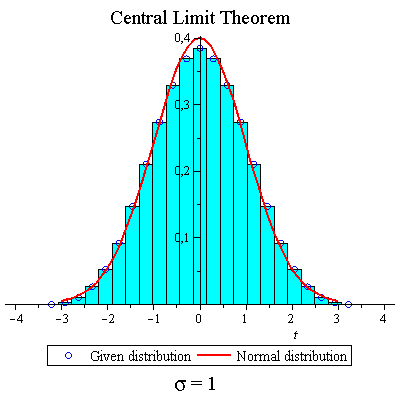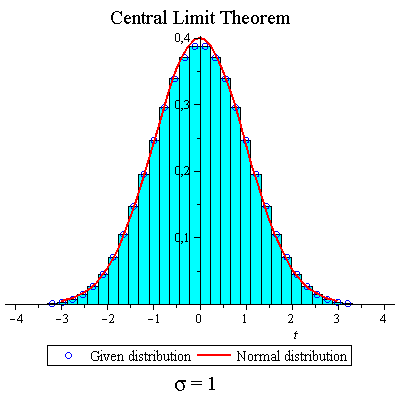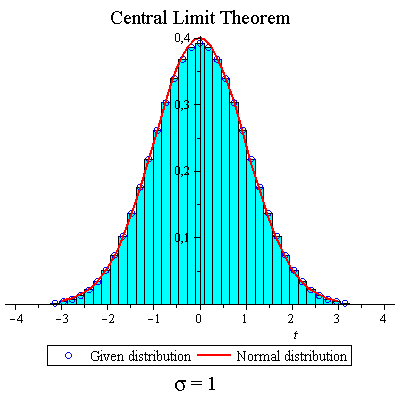 |